排序是指将集合中的元素按某种顺序排列的过程。

分析排序过程：

  • 首先，排序算法要能比较大小。为了给一个集合排序，需要某种系统化的比较方法，以检查元素的排列是否违反了顺序。在衡量排序过程时，最常用的指标就是总的比较次数。
  • 其次，当元素的排列顺序不正确时，需要交换它们的位置。交换是一个耗时的操作，总的交换次数对于衡量排序算法的总体效率来说也很重要。

快速总结：

  • 冒泡排序、选择排序和插入排序都是 $O(n^{2})$ 算法。
  • 希尔排序通过给子列表排序，改进了插入排序。它的时间复杂度介于 $O(n)$ 和 $O(n^{2})$ 之间。
  • 归并排序的时间复杂度是 $O(n\log n)$，但是归并过程需要用到额外的存储空间。
  • 快速排序的时间复杂度是 $O(n\log n)$，但当分割点不靠近列表中部时会降到 $O(n^{2})$。它不
    需要使用额外的存储空间。

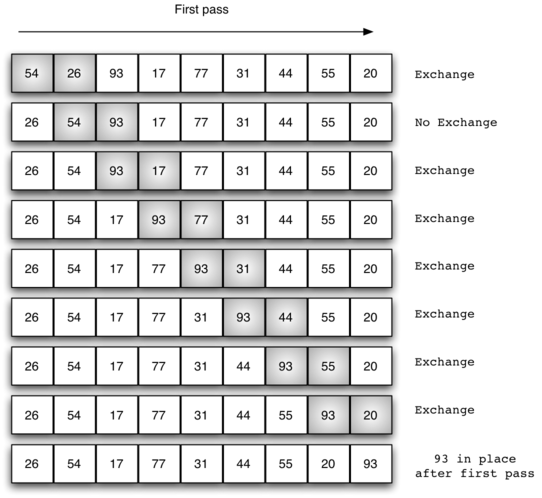
冒泡排序

冒泡排序：多次遍历列表，比较相邻的元素，将不合顺序的交换。每一轮遍历都将下一个最
大值放到正确的位置上。本质上，每个元素通过“冒泡”找到自己所属的位置。

python_sorting_fig_1.png

冒泡排序函数 bubbleSort：

def bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        for i in range(passnum):
            if alist[i]>alist[i+1]:
                temp = alist[i]
                alist[i] = alist[i+1]
                alist[i+1] = temp

冒泡排序中每一轮的比较次数：

轮次 比较次数
$1$ $n–1$
$2$ $n–2$
$3$ $n–3$
$\vdots$ $\vdots$
$n–1$ $1$

上表展示了每一轮的比较次数，总的比较次数是前 $n–1$ 个整数之和，即 $\frac{1}{2}n^{2} - \frac{1}{2}n$。该算法的时间复杂度是 $O(n^{2})$。

冒泡排序通常被认为是效率最低的排序算法，因为在确定最终的位置前必须交换元素。“多余”的交换操作代价很大。

短冒泡：如果在一轮遍历中没有发生元素交换，就可以确定列表已经有序。可以修改冒泡排序函数，使其在遇到这种情况时提前终止。

def shortBubbleSort(alist):
    exchanges = True
    passnum = len(alist)-1
    while passnum > 0 and exchanges:
       exchanges = False
       for i in range(passnum):
           if alist[i]>alist[i+1]:
               exchanges = True
               temp = alist[i]
               alist[i] = alist[i+1]
               alist[i+1] = temp
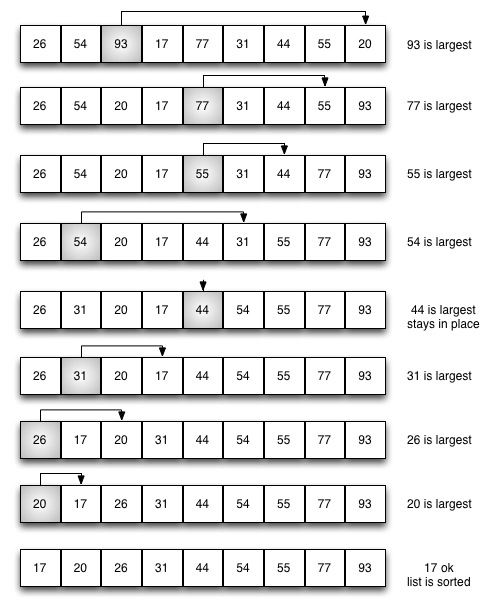
       passnum = passnum-1

选择排序

选择排序：在冒泡排序的基础上做了改进，每次遍历列表时只做一次交换，在每次遍历时寻找最大值，并在遍历完之后将它放到正确位置上。

python_sorting_fig_2.png

选择排序函数 selectionSort：

def selectionSort(alist):
   for fillslot in range(len(alist)-1,0,-1):
       positionOfMax=0
       for location in range(1,fillslot+1):
           if alist[location]>alist[positionOfMax]:
               positionOfMax = location

       temp = alist[fillslot]
       alist[fillslot] = alist[positionOfMax]
       alist[positionOfMax] = temp

选择排序算法和冒泡排序算法的比较次数相同，所以时间复杂度也是 $O(n^{2})$。但是，由于减少了交换次数，因此选择排序算法通常更快。

插入排序

插入排序：在列表较低的一端维护一个有序的子列表，并逐个将每个新元素“插入”这个子列表。

python_sorting_fig_3.png

插入排序函数 insertionSort：

def insertionSort(alist):
   for index in range(1,len(alist)):

       currentvalue = alist[index]
       position = index

       while position>0 and alist[position-1]>currentvalue:
           alist[position]=alist[position-1]
           position = position-1

       alist[position]=currentvalue

在给 $n$ 个元素排序时，插入排序算法需要遍历 $n–1$ 轮。循环从位置 $1$ 开始，直到位置 $n–1$ 结束，这些元素都需要被插入到有序子列表中。在最坏情况下，插入排序算法的比较次数是前 $n–1$ 个整数之和，对应的时间复杂度是 $O(n^{2})$。

希尔排序

希尔排序也称“递减增量排序”，它对插入排序做了改进，将列表分成数个子列表，并对每一个子列表应用插入排序。如何切分列表是希尔排序的关键——并不是连续切分，而是使用增量 $i$（有时称作步长）选取所有间隔为 $i$ 的元素组成子列表。

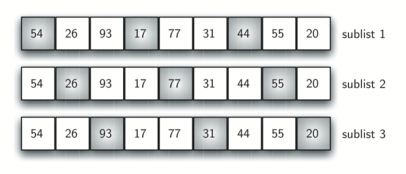
python_sorting_fig_4.png
上图为增量为 3 的希尔排序

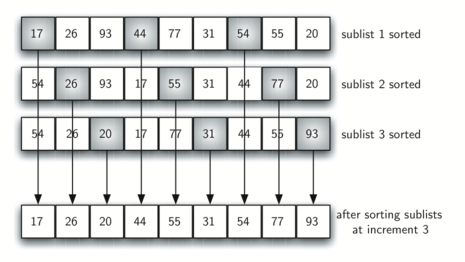
python_sorting_fig_5.png
上图为每个子列表排序后的结果

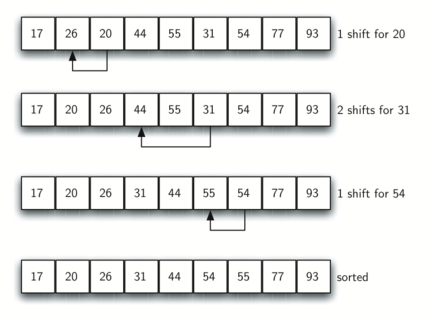
python_sorting_fig_6.png
最终进行插入排序

希尔排序函数 shellSort：

def shellSort(alist):
    sublistcount = len(alist)//2
    while sublistcount > 0:

        for startposition in range(sublistcount):
            gapInsertionSort(alist,startposition,sublistcount)

        print("After increments of size",sublistcount,
                                   "The list is",alist)

        sublistcount = sublistcount // 2

def gapInsertionSort(alist,start,gap):
    for i in range(start+gap,len(alist),gap):

        currentvalue = alist[i]
        position = i

        while position>=gap and alist[position-gap]>currentvalue:
            alist[position]=alist[position-gap]
            position = position-gap

        alist[position]=currentvalue

上述代码中的函数先为$\frac {n}{2}$个子列表排序，接着是$\frac {n}{4}$个子列表。最终，整个列表由基本的插入排序算法排好序。

希尔排序的时间复杂度大概介于 $O(n)$ 和 $O(n^{2})$ 之间。若采用上述代码中的增量，则时间复杂度是 $O(n^{2})$ 。通过改变增量，比如采用 $2^{k}-1$（$1, 3, 7, 15, 31, …$），希尔排序的时间复杂度可以达到 $O(n^{\frac {3}{2}})$。

归并排序

归并排序：它是递归算法，采用分治策略，每次将一个列表一分为二。如果列表为空或只有一个元素，那么从定义上来说它就是有序的（基本情况）。如果列表不止一个元素，就将列表一分为二，并对两部分都递归调用归并排序。当两部分都有序后，就进行归并这一基本操作。

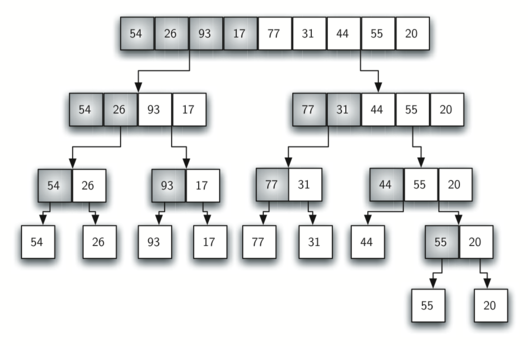
python_sorting_fig_7.png
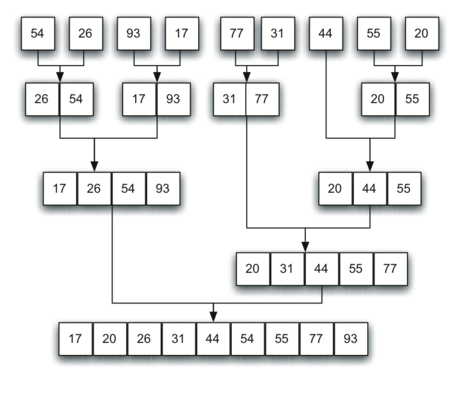
python_sorting_fig_8.png

归并排序函数 mergeSort：

def mergeSort(alist):
    print("Splitting ",alist)
    if len(alist)>1:
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i=0
        j=0
        k=0
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] <= righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i < len(lefthalf):
            alist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j < len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1
    print("Merging ",alist)

首先，列表被一分为二，当列表的长度为 $n$ 时，能切分 $\log_{2} n$ 次。第二个处理过程是归并，列表中的每个元素最终都得到处理，并被放到有序列表中。所以，得到长度为 $n$ 的列表需要进行 $n$ 次操作。由此可知，需要进行 $\log n$ 次拆分，每一次需要进行 $n$ 次操作，所以一共是 $n\log n$ 次操作。也就是说，归并排序算法的时间复杂度是 $O(n\log n)$。

注意：mergeSort 函数需要额外的空间来存储切片操作得到的两半部分。当列表较大时，使用额外的空间可能会使排序出现问题。

快速排序

快速排序：采用分治策略，但不使用额外的存储空间。首先选出一个基准值，简单起见，选取列表中的第一个元素。基准值的作用是帮助切分列表。在最终的有序列表中，基准值的位置通常被称作分割点，算法在分割点切分列表，以进行对快速排序的子调用。

python_sorting_fig_9.png
在上图中，元素 $54$ 将作为第一个基准值。

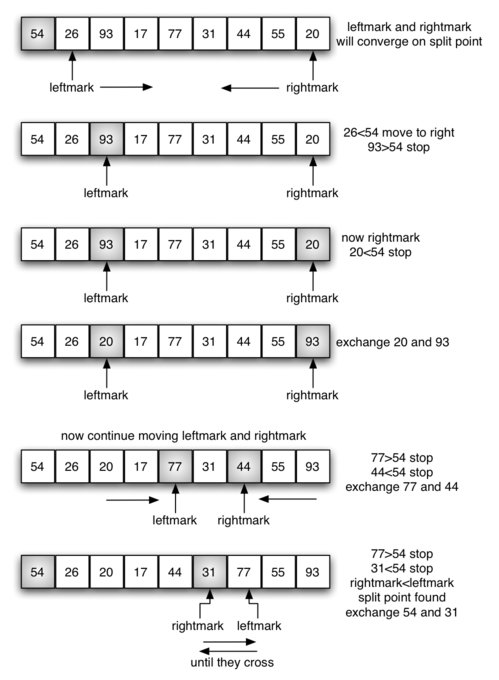
python_sorting_fig_10.png
分区操作：首先找到两个坐标——leftmark 和 rightmark。它们分别位于列表剩余元素的开头和末尾，如上图所示。分区的目的是根据待排序元素与基准值的相对大小将它们放到正确的一边，同时逐渐逼近分割点。上图展示了为元素 $54$ 寻找正确位置的过程。

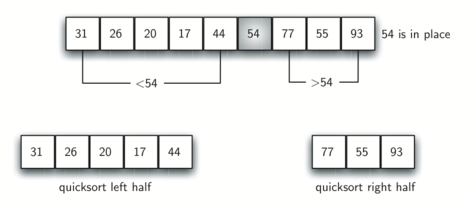
python_sorting_fig_11.png
分割点左边的所有元素都小于基准值，右边的所有元素都大于基准值。因此，可以在分割点处将列表一分为二，并针对左右两部分递归调用快速排序函数。

快速排序函数 quickSort：

def quickSort(alist):
   quickSortHelper(alist,0,len(alist)-1)

def quickSortHelper(alist,first,last):
   if first<last:

       splitpoint = partition(alist,first,last)

       quickSortHelper(alist,first,splitpoint-1)
       quickSortHelper(alist,splitpoint+1,last)


def partition(alist,first,last):
   pivotvalue = alist[first]

   leftmark = first+1
   rightmark = last

   done = False
   while not done:

       while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
           leftmark = leftmark + 1

       while alist[rightmark] >= pivotvalue and rightmark >= leftmark:
           rightmark = rightmark -1

       if rightmark < leftmark:
           done = True
       else:
           temp = alist[leftmark]
           alist[leftmark] = alist[rightmark]
           alist[rightmark] = temp

   temp = alist[first]
   alist[first] = alist[rightmark]
   alist[rightmark] = temp


   return rightmark

快速排序函数 quickSort 调用了递归函数 quickSortHelper。quickSortHelper 首先处理和归并排序相同的基本情况。如果列表的长度小于或等于 $1$，说明它已经是有序列表；如果长度大于 $1$，则进行分区操作并递归地排序。分区函数 partition 实现了前面描述的过程。

对于长度为 $n$ 的列表，分析 quickSort 函数：

  • 如果分区操作总是发生在列表的中部，就会切分 $\log n$ 次。为了找到分割点， $n$ 个元素都要与基准值比较。所以，时间复杂度是 $O(n\log n)$。

  • 分割点不在列表的中部，而是偏向某一端，这会导致切分不均匀。含有 $n$ 个元素的列表可能被分成一个不含元素的列表与一个含有 $n–1$ 个元素的列表。然后，含有 $n–1$ 个元素的列表可能会被分成不含元素的列表与一个含有 $n–2$ 个元素的列表，依此类推。这会导致时间复杂度变为 $O(n^{2})$。

三数取中法：避免切分不均匀，即在选择基准值时考虑列表的头元素、中间元素与尾元素。

文章目录