[Python] 搜索
搜索
快速总结:
- 不论列表是否有序,顺序搜索算法的时间复杂度都是 $O(n)$。
- 对于有序列表来说,二分搜索算法在最坏情况下的时间复杂度是 $O(\log n)$。
- 基于散列表的搜索算法可以达到常数阶。
Python 提供了运算符 in,通过它可以方便地检查元素是否在列表中。
>>> 15 in [3, 5, 2, 4, 1]
False
>>> 3 in [3, 5, 2, 4, 1]
True
>>>顺序搜索
无序列表的顺序搜索
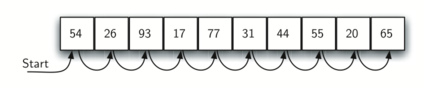
上图展示了无序列表顺序搜索的原理。从列表中的第一个元素开始,沿着默认的顺序逐个查看,直到找到目标元素或者查完列表。如果查完列表后仍没有找到目标元素,则说明目标元素不在列表中。
假设元素的排列是无序的,要确定目标元素不在列表中,唯一的方法就是将它与列表中的每个元素都比较一次,所以顺序搜索算法的时间复杂度是 $O(n)$。
def sequentialSearch(alist, item):
pos = 0
found = False
while pos < len(alist) and not found:
if alist[pos] == item:
found = True
else:
pos = pos+1
return found这个函数接受列表与目标元素作为参数,并返回一个表示目标元素是否存在的布尔值。布尔型变量
found的初始值为False,如果找到目标元素,就将它的值改为True。
有序列表的顺序搜索
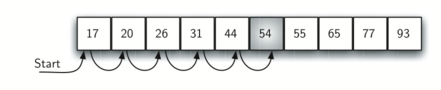
假设列表中的元素按升序排列,上图展示了无序列表顺序搜索的原理。如果存在目标元素,那么它出现在 n 个位置中任意一个位置的可能性仍然一样大,因此比较次数与在无序列表中相同,算法的时间复杂度仍是 $O(n)$。不过,如果不存在目标元素,那么搜索效率就会提高。
def orderedSequentialSearch(alist, item):
pos = 0
found = False
stop = False
while pos < len(alist) and not found and not stop:
if alist[pos] == item:
found = True
else:
if alist[pos] > item:
stop = True
else:
pos = pos+1
return found有序列表的二分搜索
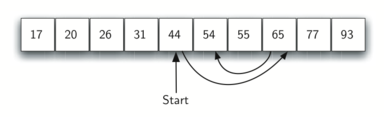
二分搜索不是从第一个元素开始搜索列表,而是从中间的元素着手。如果这个元素就是目标元素,那就立即停止搜索;如果不是,则可以利用列表有序的特性,排除一半的元素。
def binarySearch(alist, item):
first = 0
last = len(alist)-1
found = False
while first<=last and not found:
midpoint = (first + last)//2
if alist[midpoint] == item:
found = True
else:
if item < alist[midpoint]:
last = midpoint-1
else:
first = midpoint+1
return found二分搜索的递归版本:
def binarySearch(alist, item):
if len(alist) == 0:
return False
else:
midpoint = len(alist)//2
if alist[midpoint]==item:
return True
else:
if item<alist[midpoint]:
return binarySearch(alist[:midpoint],item)
else:
return binarySearch(alist[midpoint+1:],item)分析二分搜索算法:
| 比较次数 | 剩余元素的近似个数 |
|---|---|
| $1$ | $\frac{n}{2}$ |
| $2$ | $\frac{n}{4}$ |
| $3$ | $\frac{n}{8}$ |
| $\vdots$ | $\vdots$ |
| $i$ | $\frac{n}{2^i}$ |
拆分足够多次后,会得到只含一个元素的列表。这个元素要么就是目标元素,要么不是。无
论是哪种情况,计算工作都已完成。要走到这一步,需要比较 i 次,其中 $\frac{n}{2^i}=1$。由此可得,$i=\log n$。所以,二分搜索算法的时间复杂度是 $O(\log n) 。
散列
散列表是元素集合,其中的元素以一种便于查找的方式存储。散列表中的每个位置通常被称为槽,其中可以存储一个元素。槽用一个从 0 开始的整数标记,例如 0 号槽、 1 号槽、 2 号槽,等等。初始情形下,散列表中没有元素,每个槽都是空的。可以用列表来实现散列表,并将每个元素都初始化为 Python 中的特殊值 None。

上图展示了大小 m 为 11 的散列表。也就是说,表中有 m 个槽,编号从 0 到 10。
散列函数将散列表中的元素与其所属位置对应起来。对散列表中的任一元素,散列函数返回一个介于 0和 m – 1 之间的整数。下表给出了使用余数作为散列值的结果。
| 元素 | 散列值 |
|---|---|
| 54 | 10 |
| 26 | 4 |
| 93 | 5 |
| 17 | 6 |
| 77 | 0 |
| 31 | 9 |
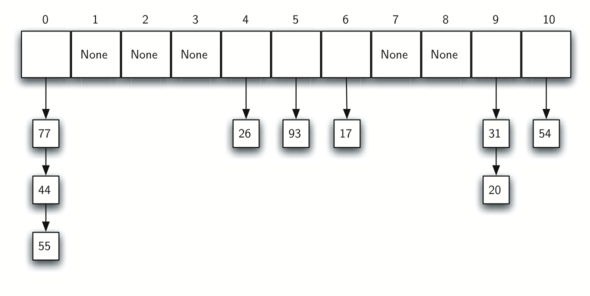
计算出散列值后,就可以将每个元素插入到相应的位置,如下图所示。

注意,在 11 个槽中,有 6 个被占用了。占用率被称作载荷因子,记作$\lambda$定义如下:
$$
\lambda = \frac {元素个数}{散列表大小}
$$
在本例中,$\lambda = \frac {6}{11}$。
搜索目标元素时,仅需使用散列函数计算出该元素的槽编号,并查看对应的槽中是否有值。因为计算散列值并找到相应位置所需的时间是固定的,所以搜索操作的时间复杂度是 $O(1)$。
散列函数
散列函数会将两个元素都放入同一个槽,这种情况被称作冲突,也叫“碰撞”。
给定一个元素集合,能将每个元素映射到不同的槽,这种散列函数称作完美散列函数。如果
元素已知,并且集合不变,那么构建完美散列函数是可能的。
我们的目标是创建一个散列函数:冲突数最少,计算方便,元素均匀分布于散列表中。
下面代码给出了 hash 函数的定义,传入一个字符串和散列表的大小,该函数会返回散列值,其取值范围是 0 到 tablesize-1。
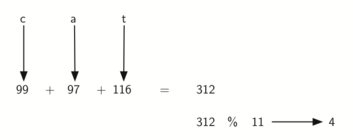
def hash(astring, tablesize):
sum = 0
for pos in range(len(astring)):
sum = sum + ord(astring[pos])
return sum%tablesize但是,针对异序词,这个散列函数总是得到相同的散列值。要弥补这一点,可以用字符位置作为权重因子。
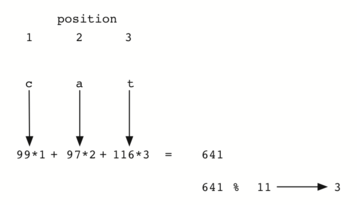
处理冲突
当两个元素被分到同一个槽中时,必须通过一种系统化方法在散列表中安置第二个元素,这个过程被称为处理冲突。
方法一:在散列表中找到另一个空槽
线性探测:简单的做法是从起初的散列值开始,顺序遍历散列表,直到找到一个空槽。注意,为了遍历散列表,可能需要往回检查第一个槽。这个过程被称为开放定址法,它尝试在散列表中逐个寻找下一个空槽或地址。
线性探测有个缺点,那就是会使散列表中的元素出现聚集现象。也就是说,如果一个槽发生太多冲突,线性探测会填满其附近的槽,而这会影响到后续插入的元素。
“加 3”探测:要避免元素聚集,一种方法是扩展线性探测,不再依次顺序查找空槽,而是跳过一些槽,这样做能使引起冲突的元素分布得更均匀。
再散列:泛指在发生冲突后寻找另一个槽的过程。
- 线性探测:再散列函数是
newhashvalue = rehash(oldhashvalue),且rehash(pos) = (pos + 1)%sizeoftable。 - “加 3”探测:再散列函数可以定义为
rehash(pos) = (pos + 3)%sizeoftable。 - 也就是说,可以将再散列函数定义为
rehash(pos) = (pos + skip)%sizeoftable。注意: “跨步”(
skip)的大小要能保证表中所有的槽最终都被访问到,否则就会浪费槽资源。要保证这一点,常常建议散列表的大小为素数。
平方探测:线性探测的一个变体,它不采用固定的跨步大小,而是通过再散列函数递增散列值。如果第一个散列值是 h,后续的散列值就是 h+1、 h+4、 h+9、 h+16,等等。
方法二:让每个槽有一个指向元素集合(或链表)的引用
链接法:允许散列表中的同一个位置上存在多个元素。发生冲突时,元素仍然被插入其散列值对应的槽中。不过,随着同一个位置上的元素越来越多,搜索变得越来越困难。
搜索目标元素时,我们用散列函数算出它对应的槽编号。由于每个槽都有一个元素集合,因此需要再搜索一次,才能得知目标元素是否存在。链接法的优点是,平均算来,每个槽的元素不多,因此搜索可能更高效。
实现映射抽象数据类型
字典是最有用的 Python 集合之一。字典是存储键–值对的数据类型。键用来查找关联的值,这个概念常常被称作映射。
映射抽象数据类型:将键和值关联起来的无序集合,其中的键是不重复的,键和值之间是一一对应的关系。映射支持以下操作:
Map()创建一个空的映射,它返回一个空的映射集合。put(key, val)往映射中加入一个新的键–值对。如果键已经存在,就用新值替换旧值。get(key)返回key对应的值。如果key不存在,则返回None。del通过del map[key]这样的语句从映射中删除键–值对。len()返回映射中存储的键–值对的数目。in通过key in map这样的语句,在键存在时返回True,否则返回False。
下面代码使用两个列表创建 HashTable 类,以此实现映射抽象数据类型。
class HashTable:
def __init__(self):
self.size = 11
self.slots = [None] * self.size
self.data = [None] * self.size名为
slots的列表用于存储键,名为data的列表用于存储值。两个列表中的键与值一一对应。在本例中,散列表的初始大小是11。散列表选为素数,可以尽可能地提高冲突处理算法的效率。
put 函数:
def put(self,key,data):
hashvalue = self.hashfunction(key,len(self.slots))
if self.slots[hashvalue] == None:
self.slots[hashvalue] = key
self.data[hashvalue] = data
else:
if self.slots[hashvalue] == key:
self.data[hashvalue] = data #replace
else:
nextslot = self.rehash(hashvalue,len(self.slots))
while self.slots[nextslot] != None and \
self.slots[nextslot] != key:
nextslot = self.rehash(nextslot,len(self.slots))
if self.slots[nextslot] == None:
self.slots[nextslot]=key
self.data[nextslot]=data
else:
self.data[nextslot] = data #replace
def hashfunction(self,key,size):
return key%size
def rehash(self,oldhash,size):
return (oldhash+1)%size
hashfunction实现了简单的取余函数。处理冲突时,采用“加 1”再散列函数的线性探测法。put函数假设,除非键已经在self.slots中,否则总是可以分配一个空槽。该函数计算初始的散列值,如果对应的槽中已有元素,就循环运行rehash函数,直到遇见一个空槽。如果槽中已有这个键,就用新值替换旧值。
get 函数:
def get(self,key):
startslot = self.hashfunction(key,len(self.slots))
data = None
stop = False
found = False
position = startslot
while self.slots[position] != None and \
not found and not stop:
if self.slots[position] == key:
found = True
data = self.data[position]
else:
position=self.rehash(position,len(self.slots))
# 确保搜索最终一定能结束,因为不会回到初始槽
# 如果遇到初始槽,就说明已经检查完所有可能的槽,并且元素必定不存在。
if position == startslot:
stop = True
return data
def __getitem__(self,key):
return self.get(key)
def __setitem__(self,key,data):
self.put(key,data)
get函数先计算初始散列值,如果值不在初始散列值对应的槽中,就使用rehash确定下一个位置。
HashTable类的最后两个方法提供了额外的字典功能。我们重载__getitem__和__setitem__,以通过[]进行访问。这意味着创建HashTable类之后,就可以使用熟悉的索引运算符了。
分析散列搜索算法
采用线性探测策略的开放定址法,搜索成功的平均比较次数如下:
$$
\frac{1}{2}\left(1+\frac{1}{1-\lambda}\right)
$$
搜索失败的平均比较次数如下:
$$
\frac{1}{2}\left(1+\left(\frac{1}{1-\lambda}\right)^2\right)
$$
采用链接法,则搜索成功的平均比较次数如下:
$$
1 + \frac {\lambda}{2}
$$
搜索失败时,平均比较次数就是 $\lambda$。
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
 疯狂的青蛙
疯狂的青蛙
评论已关闭