利用二叉堆实现优先级队列

队列有一个重要的变体，叫作优先级队列。和队列一样，优先级队列从头部移除元素，不过元素的逻辑顺序是由优先级决定的。优先级最高的元素在最前，优先级最低的元素在最后。因此，当一个元素入队时，它可能直接被移到优先级队列的头部。

我们可以使用排序函数和列表实现优先级队列。但是，就时间复杂度而言，列表的插入操作是 $O(n)$，排序操作是 $O(n\log n)$。

实现优先级队列的经典方法是使用叫作二叉堆的数据结构。二叉堆的入队操作和出队操作均可达到 $O(\log n)$。

二叉堆有两个常见的变体： 最小堆（最小的元素一直在队首）与最大堆（最大的元素一直在队首）。

我们将实现以下基本的二叉堆方法：

• BinaryHeap() 新建一个空的二叉堆。
• insert(k) 往堆中加入一个新元素。
• findMin() 返回最小的元素，元素留在堆中。
• delMin() 返回最小的元素，并将该元素从堆中移除。
• isEmpty() 在堆为空时返回 True，否则返回 False。
• size() 返回堆中元素的个数。
• buildHeap(list) 根据一个列表创建堆。

二叉堆的实现

结构属性

在实现二叉堆时，我们通过创建一棵完全二叉树来维持树的平衡。在完全二叉树中，除了最底层，其他每一层的节点都是满的。在最底层，我们从左往右填充节点。

完全二叉树可以用一个列表来表示，而不需要采用“列表之列表”或“节点与引用”表示法。由于树是完全的，因此对于在列表中处于位置 $p$ 的节点来说，它的左子节点正好处于位置 $2p$；同理，右子节点处于位置 $2p+1$。若要找到树中任意节点的父节点，只需使用 Python 的整数除法即可。给定列表中位置 $n$ 处的节点，其父节点的位置就是 $n/2$。

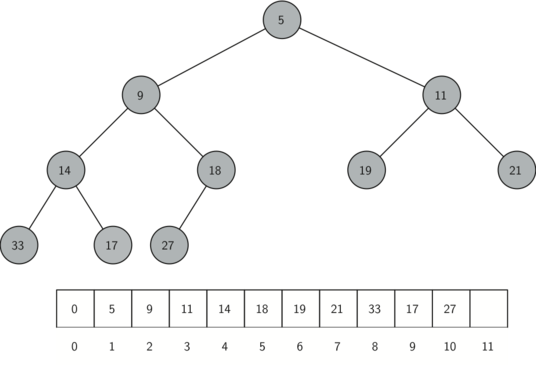
堆的有序性

我们用来存储堆元素的方法依赖于堆的有序性。
堆的有序性是指：对于堆中任意元素 $x$ 及其父元素 $p$， $p$ 都不大于 $x$。

堆操作

既然用一个列表就可以表示整个二叉堆，那么二叉堆的构造方法要做的就是初始化这个列表与属性 currentSize，用于记录堆的当前大小。

新建二叉堆：

class BinHeap:
    def __init__(self):
        self.heapList = [0]
        self.currentSize = 0

列表 heapList 的第一个元素是 0，它的唯一用途是为了使后续的方法可以使用整数除法。

将元素加入列表的最简单、最高效的方法就是将元素追加到列表的末尾。追加操作的优点在于，它能保证完全树的性质，但缺点是很可能会破坏堆的结构性质。我们可以写一个方法，通过比较新元素与其父元素来重新获得堆的结构性质。如果新元素小于其父元素，就将二者交换。

percUp 方法：

def percUp(self,i):
    while i // 2 > 0:
      if self.heapList[i] < self.heapList[i // 2]:
         tmp = self.heapList[i // 2]
         self.heapList[i // 2] = self.heapList[i]
         self.heapList[i] = tmp
      i = i // 2

该方法将元素一直沿着树向上移动，直到重获堆的结构性质。

向二叉堆中新加元素：

def insert(self,k):
    self.heapList.append(k)
    self.currentSize = self.currentSize + 1
    self.percUp(self.currentSize)

当元素被追加到树中之后，percUp 方法将其移到正确的位置。

正确定义 insert 方法后，就可以编写 delMin 方法。既然堆的结构性质要求根节点是树的最小元素，那么查找最小值就很简单。 delMin 方法的难点在于，如何在移除根节点之后重获堆的结构性质和有序性。

我们可以分两步重建堆：

1. 取出列表中的最后一个元素，将其移到根节点的位置。移动最后一个元素保证了堆的结构性质，但可能会破坏二叉堆的有序性。
2. 将新的根节点沿着树推到正确的位置，以重获堆的有序性。

将新的根节点移动到正确位置所需的一系列交换操作如下图所示：

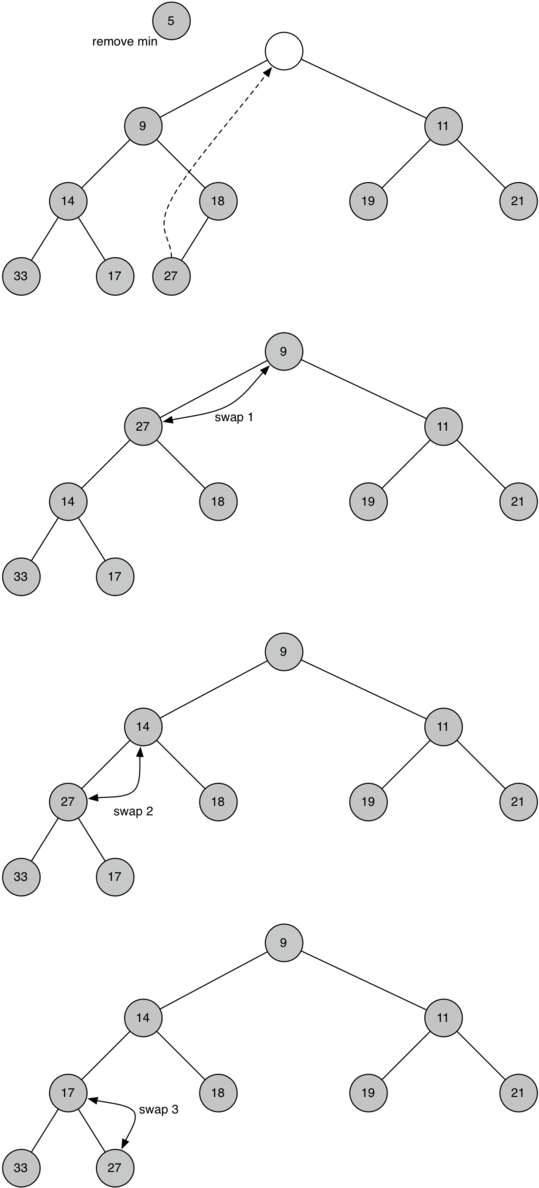
percDown 方法和 minChild 方法：

def percDown(self,i):
    while (i * 2) <= self.currentSize:
        mc = self.minChild(i)
        if self.heapList[i] > self.heapList[mc]:
            tmp = self.heapList[i]
            self.heapList[i] = self.heapList[mc]
            self.heapList[mc] = tmp
        i = mc

def minChild(self,i):
    if i * 2 + 1 > self.currentSize:
        return i * 2
    else:
        if self.heapList[i*2] < self.heapList[i*2+1]:
            return i * 2
        else:
            return i * 2 + 1

从二叉堆中删除最小的元素：

def delMin(self):
    retval = self.heapList[1]
    self.heapList[1] = self.heapList[self.currentSize]
    self.currentSize = self.currentSize - 1
    self.heapList.pop()
    self.percDown(1)
    return retval

根据元素列表构建堆：

def buildHeap(self,alist):
    i = len(alist) // 2
    self.currentSize = len(alist)
    self.heapList = [0] + alist[:]
    while (i > 0):
        self.percDown(i)
        i = i - 1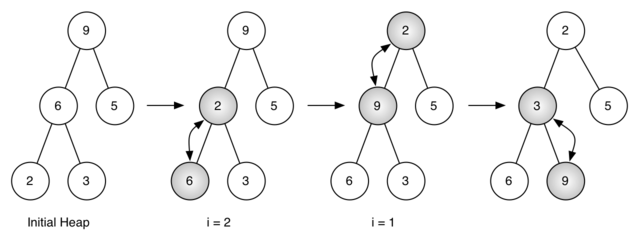

构建堆的时间复杂度是 $O(n)$。

---