平衡二叉搜索树

我们知道，当二叉搜索树不平衡时，get 和 put 等操作的性能可能降到 $O(n)$。下面将介绍一种特殊的二叉搜索树，它能自动维持平衡。这种树叫作 AVL 树，以其发明者 G. M. Adelson-Velskii 和 E. M. Landis 的姓氏命名。

AVL 树实现映射抽象数据类型的方式与普通的二叉搜索树一样，唯一的差别就是性能。实现 AVL 树时，要记录每个节点的平衡因子。我们通过查看每个节点左右子树的高度来实现这一点。更正式地说，我们将平衡因子定义为左右子树的高度之差。

$$
balanceFactor = height(leftSubTree) - height(rightSubTree)
$$

根据上述定义，如果平衡因子大于零，我们称之为左倾；如果平衡因子小于零，就是右倾；如果平衡因子等于零，那么树就是完全平衡的。为了实现 AVL 树并利用平衡树的优势，我们将平衡因子为 –1、 0 和 1 的树都定义为平衡树。一旦某个节点的平衡因子超出这个范围，我们就需要通过一个过程让树恢复平衡。下图展示了一棵右倾树及其中每个节点的平衡因子。

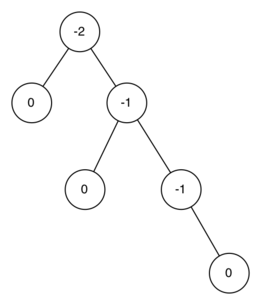
AVL 树的性能

我们先看看限定平衡因子带来的结果。我们认为，保证树的平衡因子为–1、 0 或 1，可以使关键操作获得更好的大 $O$ 性能。首先考虑平衡因子如何改善最坏情况。有左倾与右倾这两种可能性。如果考虑高度为 0、 1、 2 和 3 的树，下图展示了应用新规则后最不平衡的左倾树。

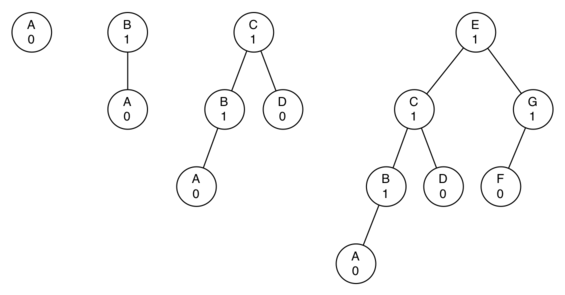
当高度为 $h$ 时，节点数 $N_h$ 是：

$$
N_h = 1 + N_{h-1} + N_{h-2}
$$

在斐波那契数列中，第 i 个数是：

$$
\begin{split}F_0 = 0 \\
F_1 = 1 \\
F_i = F_{i-1} + F_{i-2} \text{ for all } i \ge 2\end{split}
$$

随着斐波那契数列的增长， $F_i / F_{i-1}$ 逐渐逼近黄金分割比例 $\Phi$：

$$
\Phi = \frac{1 + \sqrt{5}}{2}
$$

我们将 $F_i$ 近似为 $F_i =\Phi^i/\sqrt{5}$ 。由此，可以将 $N_h$ 的等式重写为：

$$
N_h = F_{h+1} - 1, h \ge 1
$$

用黄金分割近似替换，得到：

$$
N_h = \frac{\Phi^{h+2}}{\sqrt{5}} - 1
$$

移项，两边以 $2$ 为底取对数，求 $h$，得到：

$$
\begin{split}\log{N_h+1} = (h+2)\log{\Phi} - \frac{1}{2} \log{5} \\
h = \frac{\log{N_h+1} - 2 \log{\Phi} + \frac{1}{2} \log{5}}{\log{\Phi}} \\
h = 1.44 \log{N_h}\end{split}
$$

在任何时间， AVL 树的高度都等于节点数取对数再乘以一个常数（1.44）。对于搜索 AVL 树来说，这是一件好事，因为时间复杂度被限制为 $O(\log{N})$。

AVL 树的实现

---